Tình hình là mình cũng tốt nghiệp 7 năm rồi.
Học 5 năm đại học mà kiến thức hổng nên giờ phải ngồi nghiên cứu lại mấy cái thứ đáng nhẽ ra phải nằm lòng khi ra trường.
Bài đầu tiên trong seri này mình sẽ học lại Big O.
Nội dung bài viết tham khảo chủ từ cuốn Cracking.The.Coding.Interview
Big-O
The letter O is used because the growth rate of a function is also referred to as the order of the function (wikipedia)
Một thuật toán được đánh giá là tối ưu hoá nhất thì ngoài việc phải đúng yêu cầu còn phải Dùng ít tài nguyên nhất (space complexity) và thời gian thực hiện ngắn nhất (time complexity)
Về space-complexity thì đơn giản là mình khởi tạo càng nhiều vùng nhớ để sử dụng trong giải thuật thì độ phức tạp được tính là tăng lên, sẽ ảnh huởng nhiều khi bộ nhớ máy tính có giới hạn. Mình sẽ bỏ qua chỉ tập trung vào time-complexity ở bài này.
O(1): constant time - thời gian chạy là như nhau không phụ thuộc vào dữ liệu ví dụ phép cộng, so sánh , hàm if ...
O(n): linear time - thời gian tăng dựa vào chính sác số lượng dữ liệu, ví dụ hàm duyệt từng phần tử của mảng tìm số a.
O(log n): logarithmic time - thời gian chia nửa dần, tức là sau mỗi lần chạy, số lượng phần tử giảm một nữa. ví dụ binary search, tìm từ giữa rồi qua trái hoặc qua phải để tìm tiếp trong mảng đã được sắp xếp.
O(n log n): quasilinear time -n nhân cho logn. ví dụ: heap sort, merge-sort
O(n^2): quadratic time, ví dụ duyệt mảng lồng nhau, bubble sort, insertion sort
O(2^n): exponential time, luôn luôn tránh nhưng có những lúc không thể tránh được, người ta gọi là ăn hành =)) ví dụ bài toán Tháp Hà Nội
https://en.wikipedia.org/wiki/Tower_of_Hanoi
O(n!): factorial, chạy cả ngàn năm...
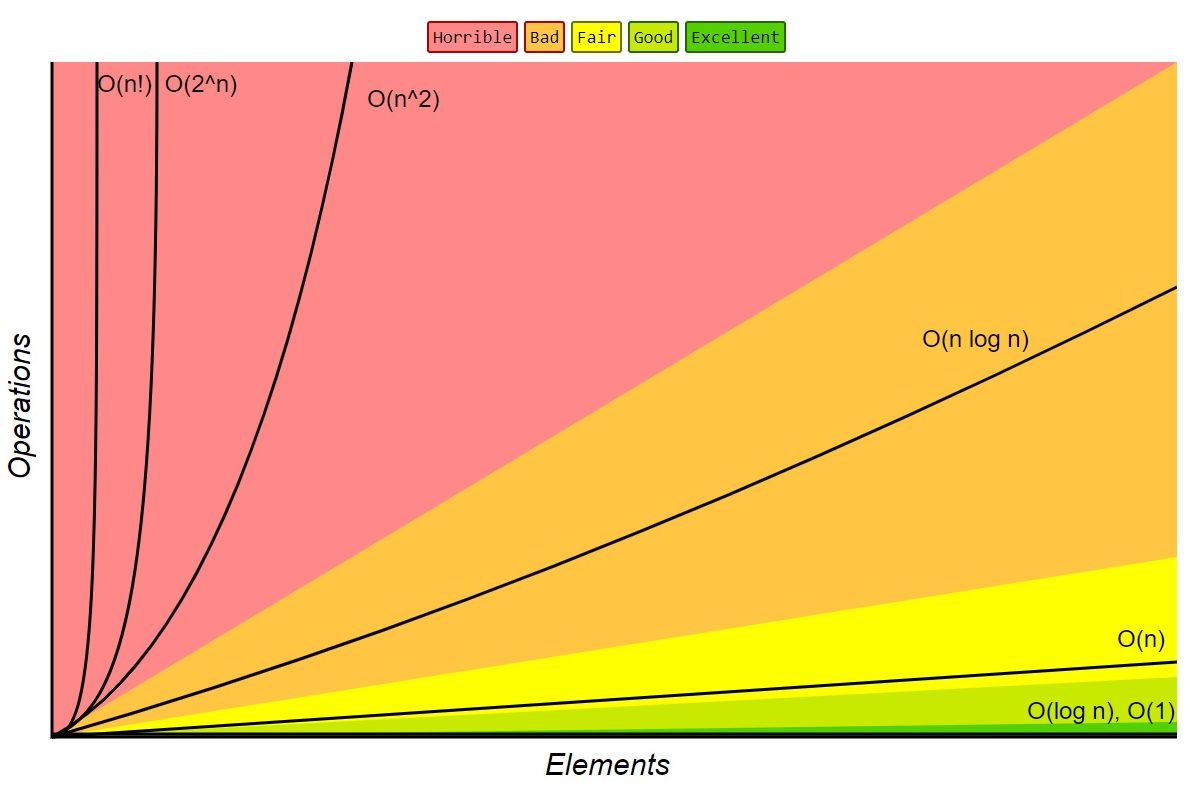
Mỗi giải thuật không phải lúc nào cũng có độ phức tạp như nhau, tuỳ thuộc vào bộ dữ liệu truyền vào hoặc giải thuật có hên hay không =))
Ví dụ: Quick sort: chọn một phần tử làm pivot, chia mảng ra 2 mảng nhỏ, 1 mảng có toàn bộ giá trị bé hơn pivot, một mảng có toàn bộ lớn hơn pivot. sau đó quicksort cho 2 mảng nhỏ. nếu chọn pivot tốt thì độ phức tạp sẽ là O(nlogn) nhưng nếu chọn xui (lúc nào cũng lớn nhất hoặc nhỏ nhất) thì sẽ là O(n^2)
Vì vậy chúng ta cần phải quan tâm thêm các case sau khi xét về time-complexity:
Best case: thời gian nhanh nhất có thể, eg: quicksort O(n) khi toàn bộ phần tử giống nhau chẳng hạn
Average case: thời gian trung bình đối với hầu hết bộ dữ liệu: eg: quicksort O(nlogn)
Worst case: thời gian tệ nhất có thể xảy ra, đã nói ở trên.
Câu hỏi đặt ra là có O(n) thì có O(2n) hay O(3n) hay O(n + 10) không?
Có, nhưng khi nói về Big O chúng ta chỉ xem xét tỉ lệ tăng theo số lượng dữ liệu đầu vào, tức là số n là số mơ hồ không chính xác là bao nhiêu, có thể rất lớn hoặc chỉ 1, chúng ta có thể bỏ các hằng số đi để đơn giản.
O(2n) tương tự O(n), O(n + 10) tương đương O(n)...
Còn một cái có thể bỏ đi nữa là chỉ lấy n có số mũ lớn nhất đối với phép cộng ví dụ:
O(n^2 + n)tương đương vớiO(n^2)có thể giải thích làO(n^2)=O(2* n^2)=O(n^2 + n^2)-> cao hơnO(n^2 + n)O(n^3 + n^2 + 10)tương đương vớiO(n^3)
Tiếp theo mình sẽ thực hành một vài ví dụ: (swift)
VD1:
func sumAndDoubleSum(_ arr: [Int]) {
var sum: Int = 0
var doubleSum: Int = 0
for value in arr {
sum += value
}
for value in arr {
doubleSum += (2 * value)
}
print(sum)
print(doubleSum)
print(doubleSum / sum)
}
Ở đây chúng ta đi qua từng phần tử của mảng 2 lần nên là O(2n) tương đương với O(n).
VD2:
func printPairs(_ arr: [Int]) {
for i in 0..<arr.count {
for j in i+1..<arr.count {
print("\(arr[i]), \(arr[j])")
}
}
}
Mặc định 2 vòng for lồng nhau chúng ta sẽ nghĩ ngay là O(n^2) nhưng có thực sự như vậy?
Phân tích kỹ hơn một chút xem sao.
Xét mỗi lần chạy vòng for ở ngoài, số lượng hàm in ở trong sẽ giảm đi một
lần đầu là n - 1, lần sau là n - 2 ..đến 1
tổng lần chạy :
n-1 + n - 2 + n - 3 + .. + 2 + 1 = n(n-1)/2 = 1/2*n^2 - 1/2*n
theo quy luật bỏ phần nhỏ hơn -> O(n^2)
VD3:
func printPairs(_ arr1: [Int], _ arr2: [Int]) {
for i in 0..<arr1.count {
for j in 0..<arr2.count {
print("\(arr1[i]), \(arr2[j])")
}
}
}
Thoạt nhìn 2 vòng for tưởng ngon ăn O(n^2) nhưng không phải =)).
Hai mảng arr1, arr2 có độ dài khác nhau hoàn toàn nên độ phức tạp thuật toán phải phụ thuộc vào cả 2. Tức là O(ab) trong đó a là số lượng phần tử trong arr1, b là số lượng trong arr2. Tương tự cho ví dụ sau
VD4:
func printPairs(_ arr1: [Int], _ arr2: [Int]) {
for i in 0..<arr1.count {
print("\(arr1[i])")
}
for j in 0..<arr2.count {
print("\(arr2[j])")
}
}
Độ phức tạp thuật toán là O(a+b)
from book:
An O(a^2) runtime is completely different from an O(a*b) runtime.
Hãy thử sơ qua một vài bài trắc nghiệm sau:
https://www.proprofs.com/quiz-school/story.php?title=bino-quest
hoặc
https://www.geeksforgeeks.org/practice-questions-time-complexity-analysis/
Happy cheating!