[Học lại] Bài 7 - DFS và BFS

DFS và BFS là hai cách duyệt đồ thị thường gặp.

Đồ thị là kiểu dữ liệu trừu tượng để cài đặt hai khái niệm trong toán học là Undirected Graph và Directed Graph
Có thể hiểu đồ thị là bản đồ của nhiều nhà (vertex) và đường đi (edge), đường đi có một chiều hoặc hai chiều.

struct Node {
    var name: String
    var children: [Node]?
}
struct Graph {
    var nodes: [Node]
}

Đối với kiểu dữ liệu tuyến tính (linear) thì để tìm kiếm một phần tử, chúng ta chỉ cần sắp xếp trước sau đó có thể giảm thời gian tìm kiếm ở các lần tiếp theo (binary search), tức là loại bỏ được một số lượng phần tử sau tìm kiếm.
Tuy nhiên đối với đồ thị, vì vị trí của các nhà là ngang hàng nhau nên để tìm nhà luôn luôn chính xác thì phải đi qua từng nhà. Hên thì gặp nhà cần tìm sớm, xui thì phải đi hết.

Trước khi vào chi tiết 2 cái giải thuật, chúng ta có 2 hàm cần quan tâm khi duyệt đồ thị

• danh sách nhà kế bên - listAdjacent(of: Node) -> [Node]
• đánh giấu nhà là đã vào xem - visitNode(_ node: Node)

OK, vào chủ đề chính:

DFS - Depth First Search
Ý tưởng: thấy n cổng vào, chọn một cái bất kỳ, đi đến khi nào hết đường mới quay trở ra và đi n-1 cái cổng còn lại tương tự. Vì cách duyệt là tương tự cho mỗi cổng và cổng con ở sâu bên trong nên dùng đệ quy (stack) là hợp lý.

func dfs(_ root: Node?) {
    guard root != nil else {
        return
    }
    
    visit(root)
    
    for node in root?.children {
        if isVisited(node) {
            continue
        }
        dfs(node)
    }
}

BFS - Breath First Search
Ý tưởng: thấy n cổng vào, chọn một cái, cho những cái còn lại vào hàng đợi,
vào cái được chọn nhưng không vào sâu hơn nữa, thấy mấy cái cổng sâu hơn cho vào hàng đợi ban đầu. Tiếp tục như vậy cho đến khi cái hàng đợi không còn cổng nào.
Lưu ý khi kiểm tra một cổng thì cần đánh giấu lại là đã bỏ các cổng con vào trong queue ( khác với visit)

func bfs(_ root: Node?) {
    var queue = Queue()
    
    mark(root) //danh dau la da bo con vao queue
    
    queue.enqueue(root)
    
    while(!queue.isEmpty()) {
        let last = queue.dequeue()
        
        visit(last)
        
        for node in last.children {
            if !isMarked(node) {
                mark(node)
                queue.enqueue(node)
            }
        }
    }
}

Cần test lại nhỉ:

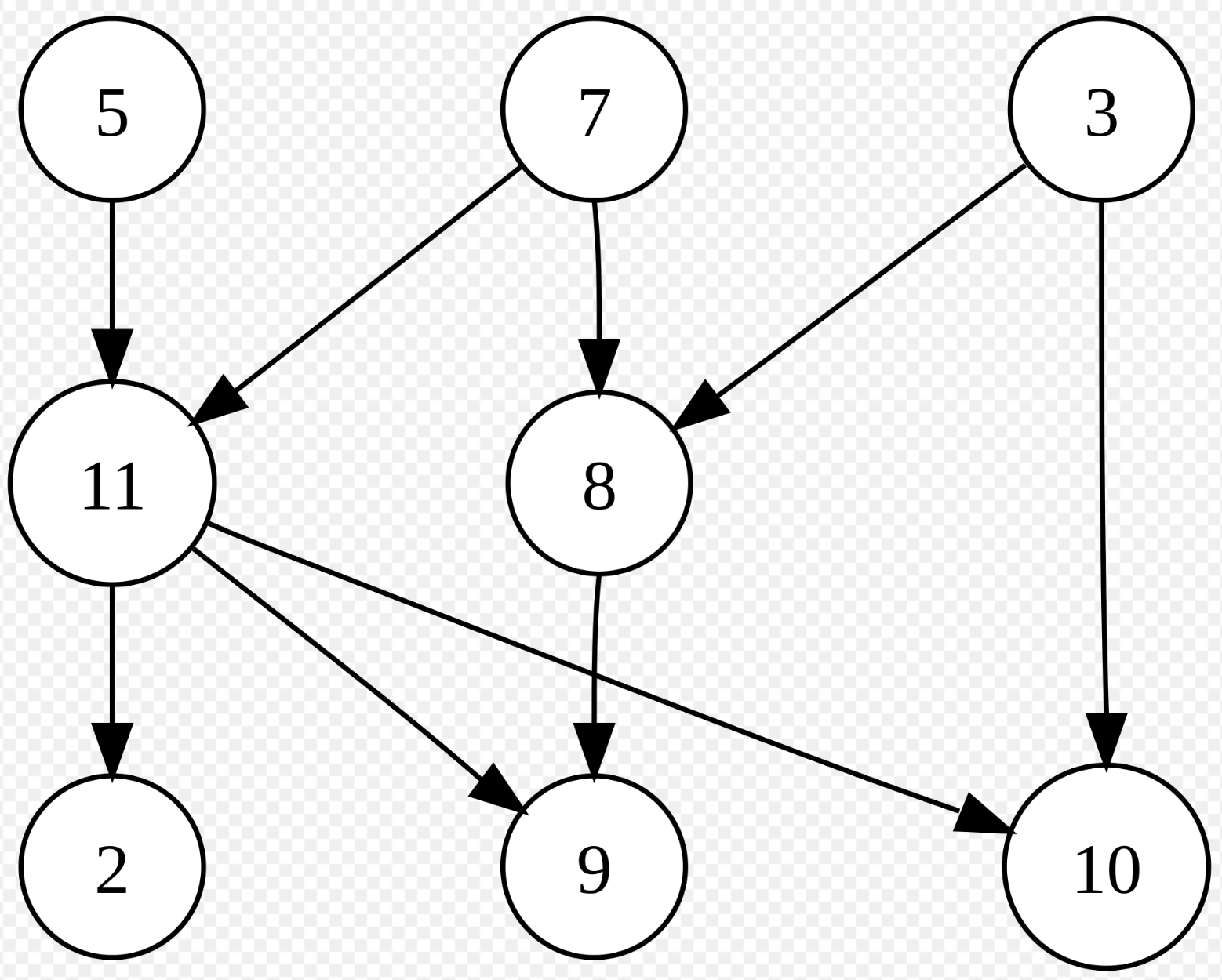
Đồ thị này có 3 root node.
DFS: 5 -> 11 -> 2 -> 9 -> 10 -> 7 -> 8 -> 3
BFS: 5 -> 7 -> 3 -> 11 -> 8 -> 2 -> 9 -> 10

Mình sẽ viết phần sau giải bài tập trong sdk =))

Happy Coding!

PlayStation5 DualSense ワイヤレスコントローラー 価格：7,678円（税込、送料無料) (2023/8/31時点)