What makes a good hashing function?

Below are my self-implement hash function follow this common way:

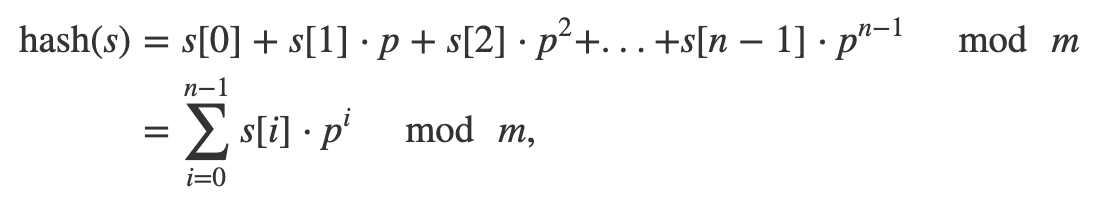
extension String {
    var myHash: UInt {
        let p: UInt = 1111991 //prime number, nearly all possible characters of str
        let m: UInt = UInt(1e9 + 11) //prime number, 
        // should be large to reduce the percentage of collision of two random strings (~ 1/m), 
        //and should be small enough to perform multiplication without overflowing (Int64)
        //https://en.wikipedia.org/wiki/Linear_congruential_generator
        
        var hashValue: UInt = 0
        var pPow: UInt = 1
        for c in self {
            let numberRepresenting = UInt(c.unicodeScalars.first!.value)
            hashValue += ((numberRepresenting * pPow) % m)
            pPow = (pPow * p) % m
        }
        return hashValue
    }
}

print("hello".myHash) //1980540924
print("thisisareally_long_string_to_compute_couldwemakeit".myHash) //23955027982
print("👏".myHash) //128079
print("1".myHash) //49
print(";".myHash) //59
print("a".myHash) //97
print("".myHash) //0
print(" ".myHash) //32

As you can see, the hash function will work with all unicode characters. It's using technique called polynomial rolling hash function.
p and m are constant, and the choice of them is important to get good hashing value. That is one element to judge a hash function, uniformly distribute the keys.

The second element to judge is the efficiently computation. Here I pre-calculate pPow, and the % function just take O(1) time complexity. Overall, the method above could satisfy O(n) where n is length of key.

Or you can reference those methods, it's simple and fast to catch up

extension String {
    var djb2hash: Int {
        let unicodeScalars = self.unicodeScalars.map { $0.value }
        return unicodeScalars.reduce(5381) {
            ($0 << 5) &+ $0 &+ Int($1)
        }
    }

    var sdbmhash: Int {
        let unicodeScalars = self.unicodeScalars.map { $0.value }
        return unicodeScalars.reduce(0) {
             Int($1) &+ ($0 << 6) &+ ($0 << 16) - $0
        }
    }
}

That's all. Happy coding.

Some extra works I tried to implement:

extension Int {
    var isPrime: Bool {
        if self % 2 == 0 {
            return false
        }
        
        let squareRoot = Int(sqrt(Double(self)))
        for i in stride(from: 3, through: squareRoot, by: 2) {
            if self % i == 0 {
                return false
            }
        }
        
        return true
    }
    
    var nearestPrime: Int {
        var goUp = self
        var goDown = self
        while true {
            goUp += 1
            goDown -= 1
            
            if goUp.isPrime {
                return goUp
            }
            if goDown.isPrime {
                return goDown
            }
        }
        return -1
    }
}

References

https://cp-algorithms.com/string/string-hashing.html
https://useyourloaf.com/blog/swift-hashable/
https://en.wikipedia.org/wiki/Rolling_hash
https://stackoverflow.com/questions/5924105/how-many-characters-can-be-mapped-with-unicode
https://www.geeksforgeeks.org/what-are-hash-functions-and-how-to-choose-a-good-hash-function/