Quy hoạch động ?

Quy hoạch động - nghe có vẻ hàn lâm nhỉ.

Đa phần tài liệu tiếng Việt mình đọc qua đều khó hiểu, nào là sum, epsilon rồi ép ít =)) mắc mệt, nên hôm nay mình sẽ thử diễn giải lại theo cách hiểu của mình và cài đặt một số giải thuật ứng dụng quy hoạch động từ đơn giản đến phức tạp bằng Swift hy vọng phần nào giúp các bạn lập trình viên nắm ý tưởng dễ dàng hơn.

Một thuật giải được coi là tốt nếu có thời gian chạy (time complexity) và bộ nhớ sử dụng (space complexity) nhỏ. Các bạn có thể xem bài trước về Big-O của mình để hiểu rõ hơn.

Quy hoạch động là một cách cài đặt thuật toán thông qua việc tăng bộ nhớ sử dụng để giảm thời gian chạy.

Thuật toán đó gồm nhiều bước giải con, và có một vài bước lặp lại nhiều lần. Với quy hoạch động chúng ta không cần giải lại bài toán con trùng lặp mà chỉ giải một lần, ghi nhớ kết quả (memoization hoặc tabulation), sau đó truy xuất kết quả cho lần kế tiếp với O(1) thời gian.

Mảng, bảng băm, hoặc bất cứ cấu trúc dữ liệu nào mà truy xuất với O(1) thời gian đều có thể dùng để lưu trữ kết quả được.

Ví dụ đơn giản dễ hiểu nhất là tìm số Fibonacci thứ n.

func fib(_ n: Int) -> Int {
    if n <= 1 { return 1 }
    return fib(n-1) + fib(n-2) // O(2^n) time
}

Với cách giải trên chúng ta có thể dễ dàng nhận thấy ở fib(n-2) đã được giải ở fib(n-1) trước đó nên khá lãng phí thời gian khi phải giải lại.

Cách cài đặt với quy hoạch động dùng bảng băm như sau:

func fib(_ n: Int) -> Int {
    var memo = [Int: Int]() // O(n) bộ nhớ dùng thêm
    return fibHelper(n, &memo) // O(n) thời gian chạy
}

func fibHelper(_ n: Int, _ memo: inout [Int: Int]) -> Int {
    // trường hợp cơ bản
    if n < 2 { return 1 }
    
    // nếu đã giải thì chỉ cần trả về
    if let solved = memo[n] { return solved } 
    
    // giải và lưu lại cho lần gọi tiếp theo
    let res = fibHelper(n - 1, &memo) + fibHelper(n - 2, &memo)
    memo[n] = res
    
    return res
}

Mình có cải tiến cách code khi dùng mảng:

//giả định n luôn >= 0
func fib(_ n: Int) -> Int {
    var memo: [Int] = Array(repeating: 0, count: n + 1)
    return fibHelper(n, &memo)
}
func fibHelper(_ n: Int, _ memo: inout [Int]) -> Int {
    if n < 2 { 
        memo[n] = 1
    } else {
        if memo[n] == 0 {
            memo[n] = fibHelper(n - 2, &memo) + fibHelper(n - 1, &memo)
        }
    }
    return memo[n]
}

Còn đây là cách giải không dùng đệ quy

func fib(_ n: Int) -> Int {
    if n < 2 { return 1 }
    var memo = Array(repeating: 1, count: n + 1)
    for i in 2...n {
        memo[i] = memo[i - 2] + memo[i - 1]
    }
    return memo[n]
}

Đối với bài toán tìm số Fibonacci này có một số cách giải tối ưu cả bộ nhớ, nhưng vì trong phạm vi liên quan quy hoạch động nên mình không liệt kê ra. Các bạn có thể xem ở link này

Quy hoạch động thường có thể kết hợp với chia để trị (mình sẽ viết bài về cái này sau) để giải một số bài toán phức tạp hơn.

Bây giờ hãy cùng mình thử giải một bài toán rối não hơn nhỉ?

1. Phân tích yêu cầu:

• n >= 0
• trả về số cây nhị phân tìm kiếm có thể tạo ra từ số n trên
  cây nhị phân tìm kiếm là cây nhị phân ( đương nhiên =)), tức là có <= 2 số cây con) và thoả điều kiện tất cả node ở cây con bên trái < root node < tất cả node bên phải.

2. Cách tiếp cận:
n số tương ứng với n node được sắp xếp tăng dần, mỗi node sẽ đảm nhiệm vị trí gốc (root) của cây ít nhất một lần, như vậy sẽ có ít nhất n + 1 cây, thử phân tích để tìm công thức chung.

Với n = 0: ta có 1 cây rỗng f(0) = 1
Với n = 1: ta có 1 cây với 1 node duy nhất f(1) = 1
Với n = 2:
lấy node 1 là root, ta giải bên trái 0 node, bên phải với số node là 1: f(0) * f(1) = 1
lấy node 2 là root, 1 node bên trái và 0 node bên phải f(1) * f(0) = 1
tổng cộng có 2 cây, f(2) = f(0) * f(1) + f(1) * f(0) = 2

dễ dàng nhận thấy, đối với mỗi trường hợp, kết quả là phép nhân của kết quả cây con bên trái và kết quả cây con bên phải.

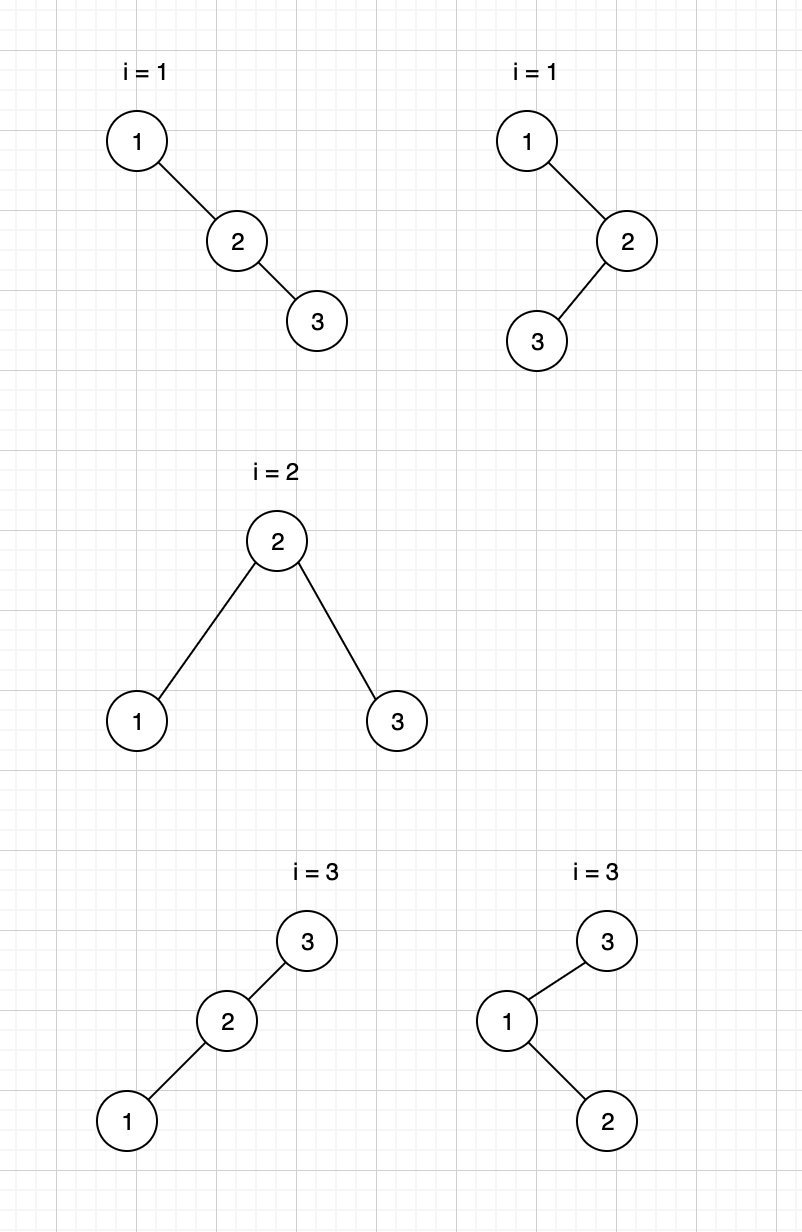
Với n = 3:
lấy node 1 root, còn 2 node bên phải: f(0) * f(2) = 2
lấy node 2 root, còn 1 bên trái và 1 bên phải: f(1) * f(1) = 1
lấy node 3 root, còn 2 node bên trái: f(2) * f(0) = 2
tổng cộng có f(2) * f(0) + f(1) * f(1) + f(0) * f(2) = 5 cây

Với n = 4:
lấy node 1 root, còn 3 node bên phải: f(0) * f(3) = 5
lấy node 2 root, còn 1 bên trái, 2 bên phải: f(1) * f(2) = 2
lấy node 3 root, còn 2 bên trái, 1 bên phải: f(2) * f(1) = 2
lấy node 4 root, còn 3 node bên trái: f(3) * f(0) = 5
tổng cộng có f(3) * f(0) + f(1) * f(2) + f(2) * f(1) + f(0) * f(3) = 14

Vậy với n >= 2 bất kỳ
lấy node thứ i, có f(i) cách giải cây con bên trái và f(n - i - 1) cách giải cây con bên phải.

4. Cài đặt
Không quy hoạch động

func numTrees(_ n: Int) -> Int {
    if n < 2 { return 1 }
    var res = 0
    for i in 0..<n {
        res += numTrees(i) * numTrees(n - i - 1)
    }
    return res
}

Cách giải trên tốn O(n^3) thời gian chạy và O(1) bộ nhớ.

Hãy xem sự lợi hại của quy hoạch động =))

func numTrees(_ n: Int) -> Int {
    var memo = [Int: Int]() // O(n) bộ nhớ
    return helper(n, &memo) // O(n^2) thời gian chạy
}

func helper(_ n: Int, _ memo: inout [Int : Int]) -> Int {
    if n < 2 { return 1 }

    if let solved = memo[n] { return solved }

    var res = 0
    for i in 0..<n {
        res += helper(i, &memo) * helper(n - i - 1, &memo)
    }
    memo[n] = res
    return res
}

Các bạn chỉ cần copy paste và gọi thêm hàm print(numTrees(10)) vào online compiler này để kiểm tra.

Dưới đây là một số bài toán có thể dùng quy hoạch động mình đang cố gắng luyện tập hàng ngày để hình thành thói quen, sau đó có thể auto giải các bài toán liên quan.
https://leetcode.com/tag/dynamic-programming/

Hy vọng qua bài này các bạn sẽ có cái nhìn đơn giản hơn về Dynamic Programming (quy hoạch động) và phần nào giúp các bạn thiết kế được giải thuật tối ưu nhất.

Happy coding and happy new year.
Thân.